-
Instead of dividing the list once, a recursive mergeSort will keep dividing the list in half until the sublists are one or two values in length.
-
When developing a recursive solution, a key step is identifying the base case of the solution. What situation will terminate the recursion? In this case, a sublist of one or two values will be our two base cases.
- Let's try and work through the recursive mergeSort of a list of eight values.
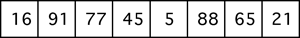
The list is divided into two sublists:

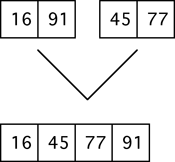
Now let's work on the left sublist. It will be divided into lists of two.

Each list of two is now very easy to sort. After each list of two is sorted, we then merge these two lists back into a list of four.
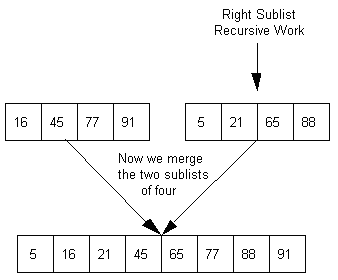
Now the algorithm proceeds to solve the right sublist (positions 5-8) recursively. Then the two lists of four are merged back together.